Topological photonics is a rapidly growing interdisciplinary field that explores precise and robust techniques to manipulate the flow of light by applying the theory of topology in material physics. Condensed matter topological insulators are exotic band gap materials that support conducting states on their surfaces but insulate in the bulk. These conducting states are topologically protected — they propagate robustly against certain types of defects. As the counterparts to electronic topological insulators, photonic topological insulators allow robust light flow only on the surface or periphery. Recently, research in topological photonics not only helps us understand how light waves can be controlled and manipulated and explore how novel optical effects can be synthesized; but also result in more efficient optical components including waveguides, lasers, optical filters, etc. that can be used to create more efficient solar cells, more powerful computer chips, and more stable quantum photonic platforms.
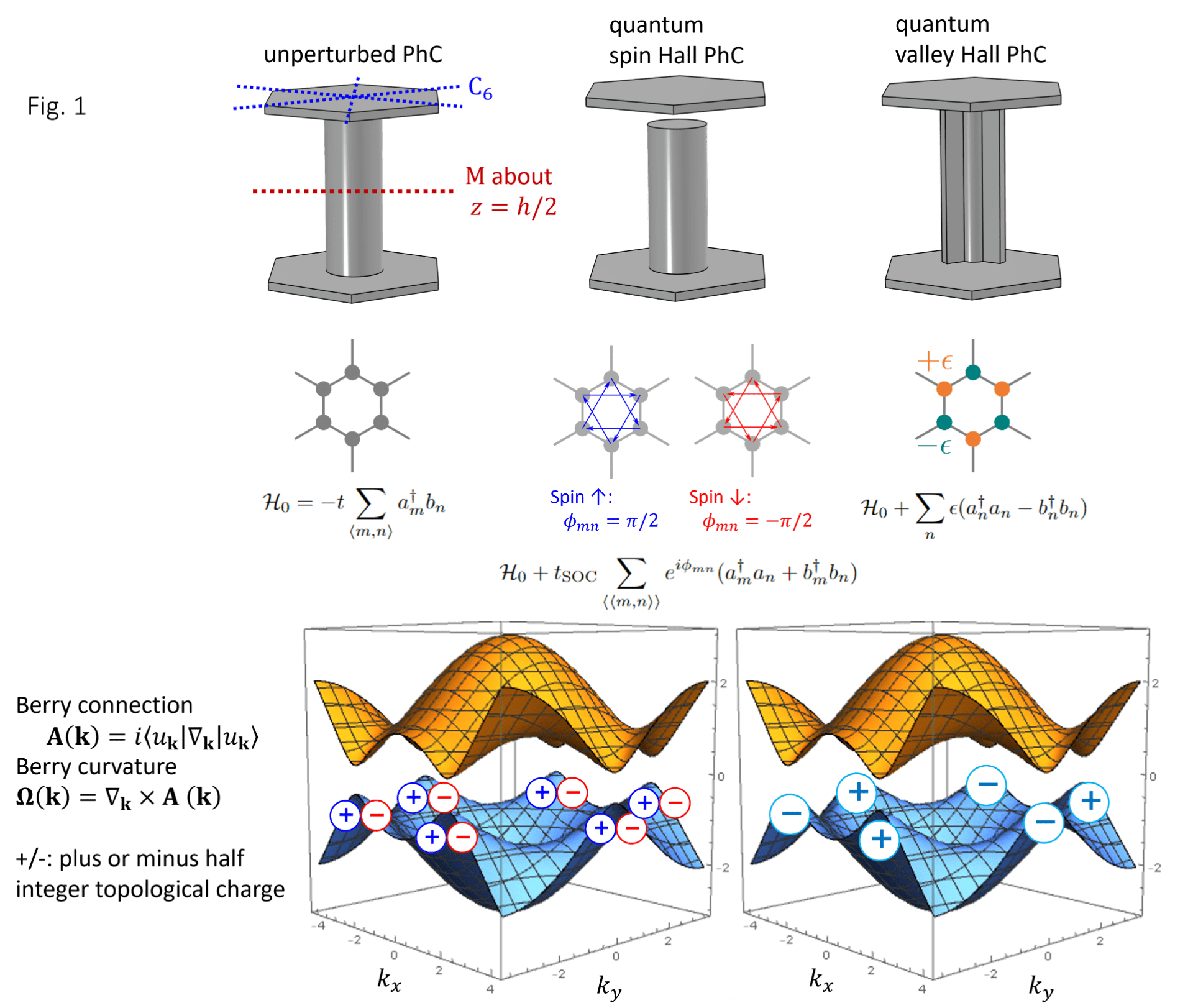
Our group proposed RF quasi-2D photonic crystals (PhCs) that realize photonic analogs of the quantum spin Hall and the quantum valley Hall effects [1,2,3]. We started from a triangular lattice of metallic rods between two parallel plates. This system hosts two important symmetries: one is the C6 rotational symmetry (in the xy-plane) which is granted by the triangular crystalline lattice; the other is the mirror symmetry with respect to the plane at h/2 (Figure 1). By breaking different symmetries of this lattice, we realized different topological insulating phases. For example, the valley Hall phase is realized by breaking the inversion symmetry; the spin Hall phase is realized by introducing an artificial bianisotropy to hybridize the TE and TM polarizations. The broken symmetry opens a photonic band gap that is topologically nontrivial — locally concentrated Berry curvature sums to plus or minus half-integer topological charges at the non-equivalent valleys of the Brillouin zone.
[1] Alexander B. Khanikaev, S. Hossein Mousavi, Wang-Kong Tse, Mehdi Kargarian, Allan H. MacDonald & Gennady Shvets. Photonic topological insulators. Nature Materials 12, 233–239 (2013). https://doi.org/10.1038/nmat3520
[2] Tzuhsuan Ma, Alexander B. Khanikaev, S. Hossein Mousavi, and Gennady Shvets. Guiding Electromagnetic Waves around Sharp Corners: Topologically Protected Photonic Transport in Metawaveguides. Physical Review Letters 114, 127401 (2015). https://doi.org/10.1103/PhysRevLett.114.127401
[3] Tzuhsuan Ma and Gennady Shvets. Scattering-free edge states between heterogeneous photonic topological insulators. Physical Review B 95, 165102 (2017). https://doi.org/10.1103/PhysRevB.95.165102
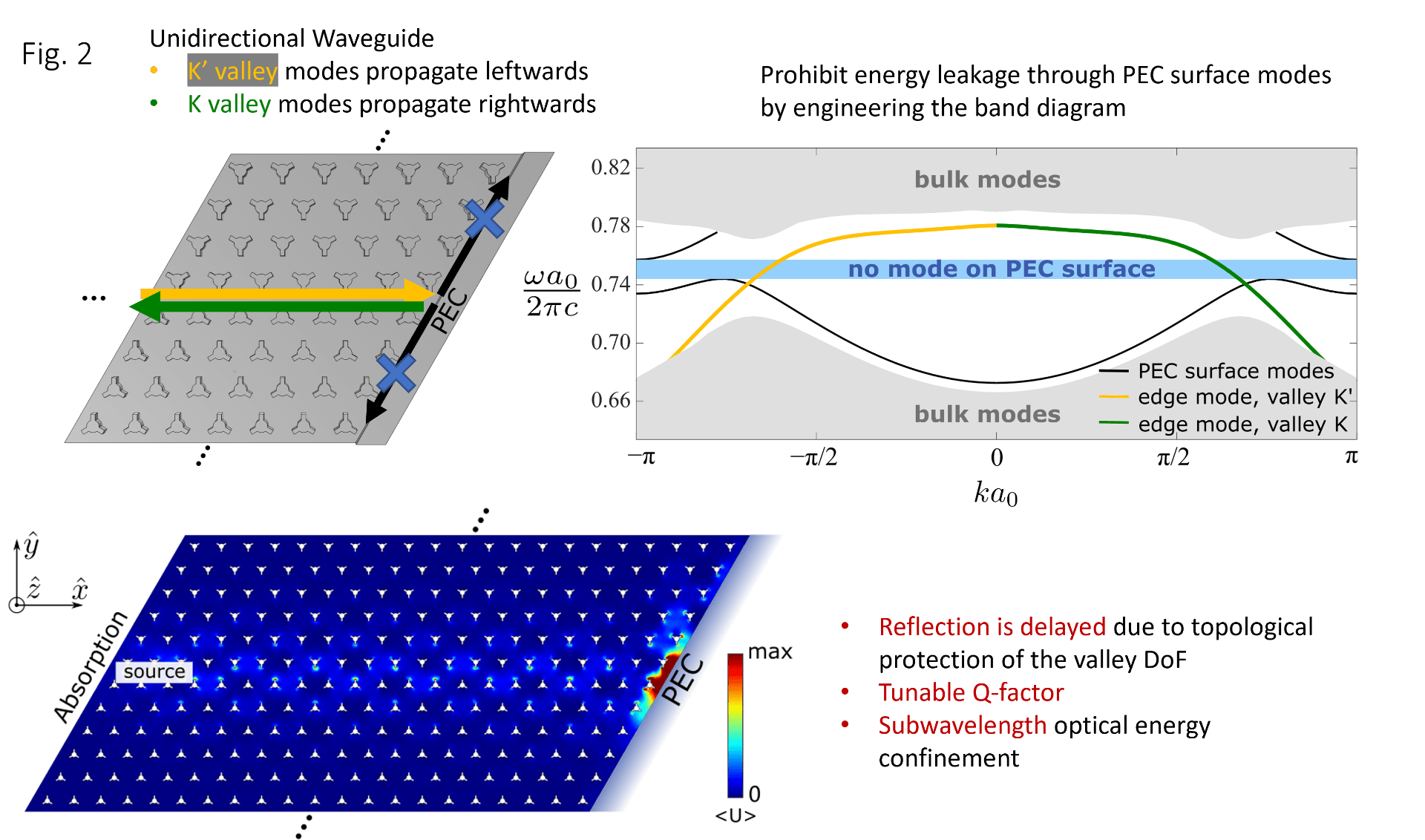
Recently, our group started to extend the research of topological photonics toward applications and more complicated topological phases. In 2020, we demonstrated a topological cavity based on the near-conservation of the valley degree of freedom [4]. We abruptly terminate a topological waveguide that supports unidirectional valley-polarized light propagation. Usually, the light will escape the structure along the surface of the termination. We precisely engineer the photonic band structure and create a “no-surface-mode” band gap where those leakage channels are prohibited. Operating at this “no-surface-mode” frequency spectrum, the only possible channel for the input light to enter is the back-reflection. However, a reflection requires a flip of the topological valley index, which requires a precise momentum jump. As the optical energy localizes at the termination, the photon position becomes well-defined, and its momentum becomes ill-defined, according to the uncertainty principle. Hence, a momentum jump is provided, and the photon’s valley index is flipped, resulting in a back-reflection.
We demonstrated a nanophotonic design based on the same principle, which can be integrated into all-dielectric photonic chips. This topological cavity can find applications in photonic information storage and processing.
[4] Yandong Li, Yang Yu, Fengyu Liu, Baile Zhang, and Gennady Shvets. Topology-Controlled Photonic Cavity Based on the Near-Conservation of the Valley Degree of Freedom. Physical Review Letters 125, 213902 (2020). https://doi.org/10.1103/PhysRevLett.125.213902
Our group’s research on topological photonics also covers the burgeoning field of higher-order topological insulators (HOTIs). A d-dimensional HOTI can support (d-d’)-dimensional topological states, where d-d’>=2. Compared to regular topological insulators (TIs) which support topological edge states, 2D HOTIs host topological 0D corner states, and 3D HOTIs host 1D hinge states.
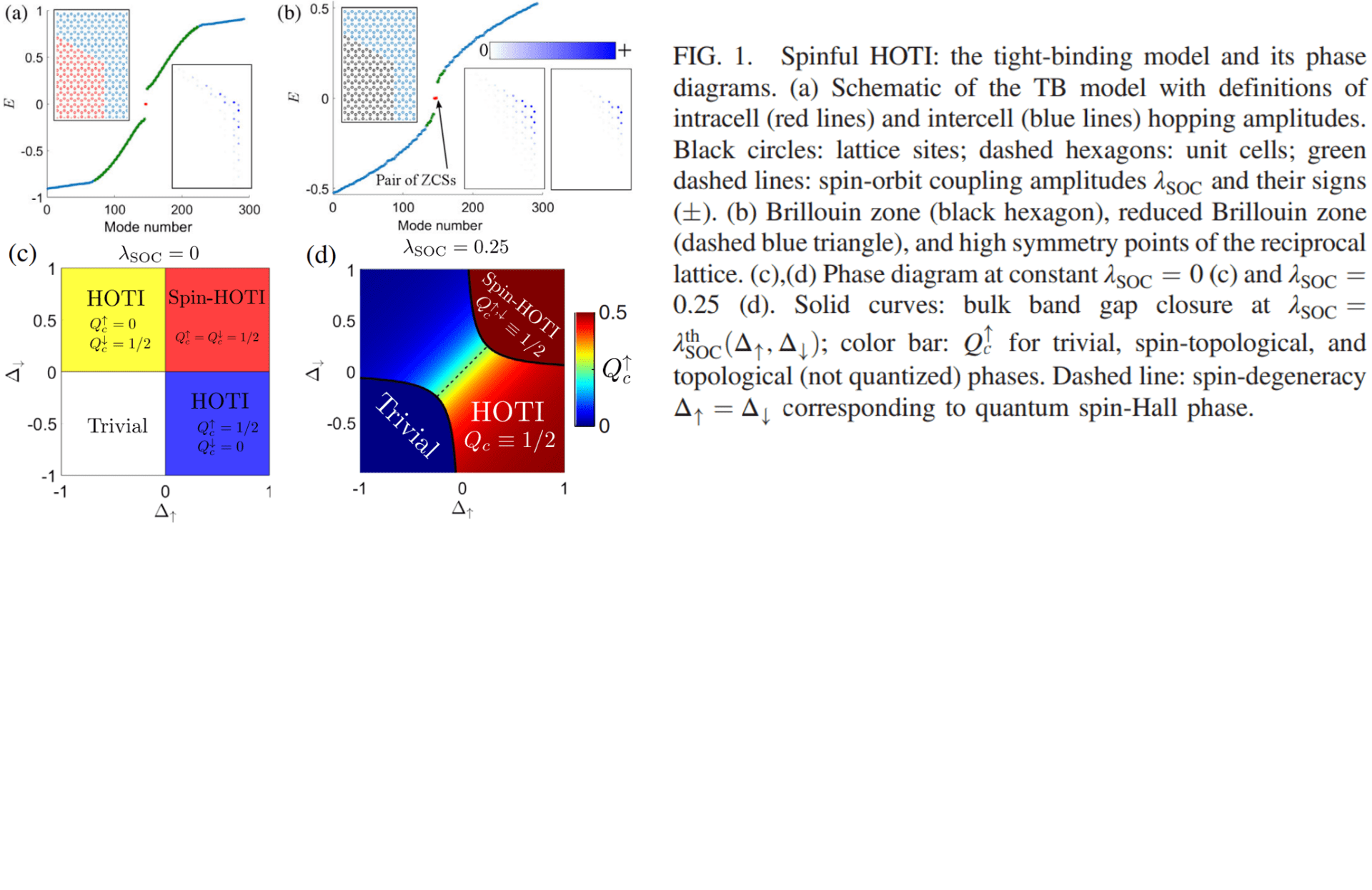
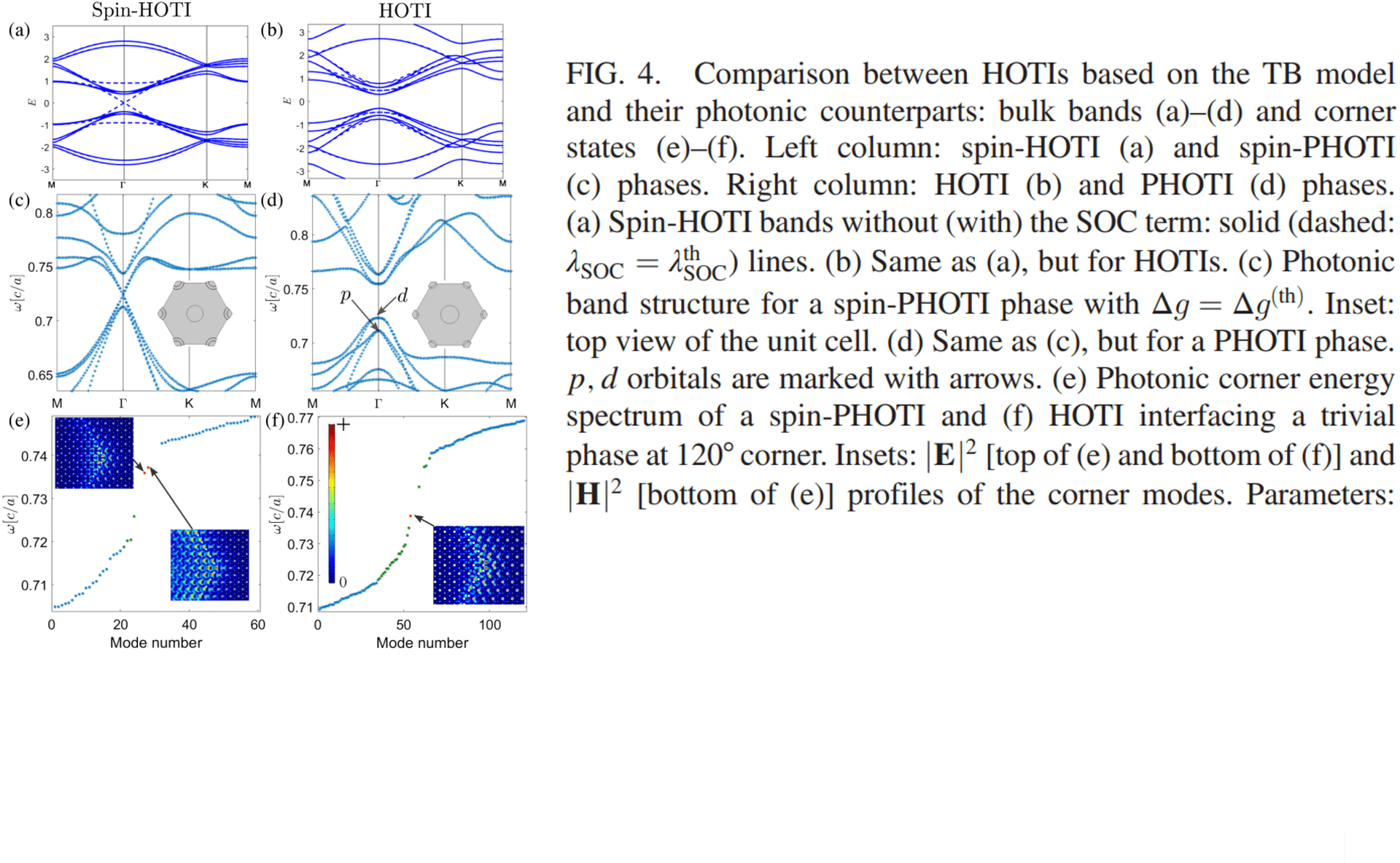
In 2022, our group introduced an artificial spin subspace to a HOTI and demonstrated a phase transition from a single fractional corner charge to a pair of spin-dependent fractional corner charges. We used a tight-binding model to analyze the phase transition. The coupling between the two spins is implemented as a Kane-Mele next-nearest neighbor spin-orbit coupling term. Fig. 3(c,d) demonstrates the phase diagram for different spin-orbit coupling terms. The spinful HOTI phase is characterized by the two zero-energy corner states (ZCS). We also proposed a photonic structure with a new type of synthetic pseudospin that realized the two different phases demonstrated in the tight-binding model (Fig. 4).
[5] Ran Gladstein Gladstone, Minwoo Jung, and Gennady Shvets. Spin-Polarized Fractional Corner Charges and Their Photonic Realization. Physical Review Letters 128, 026801 (2022). https://doi.org/10.1103/PhysRevLett.128.026801